Introduction
The effect of rolling resistance mechanisms at particle contacts and associated energy dissipation may be of major importance for many granular applications, both in the dense quasistatic regime or in dynamic regimes. In real granular systems, these mechanisms may have different micro-mechanical origins, such as adhesion on the contact area, or steric effect due to surface roughness or non-sphericity about the contact point. The rolling resistance contact model provided in PFC is a simple model, based on the linear model, that incorporates a torque acting on the contacting pieces and resisting rolling motion. It is based on the review paper by Ai et al. (2011) and on the work presented by Wensrich and Katterfeld (2012). The user is encouraged to consult these papers and references therein for a good introduction to the importance of rolling resistance mechanisms in granular applications and their implementation in DEM numerical models.
Behavior Summary
The behavior of the rolling resistance linear contact model is similar to that of the linear model, except that the internal moment is incremented linearly with accumulated relative rotation of the contacting pieces at the contact point up to a limiting value equal to the current normal force times a rolling resistance coefficient times an effective contact radius. The constant that relates the increment of internal moment to the increment of relative rotation at the contact point, denoted as rolling stiffness, is related to the shear stiffness and to the effective radius of the contact following Iwashita and Oda (1998). As discussed by Wensrich and Katterfeld (2012), this choice sets the nominal rotational natural frequency due to the rolling stiffness equal to the nominal rotational natural frequency due to the shear stiffness, and leads to a well-behaved and well-damped rolling resistance mechanism without the need for an additional damping parameter. The rolling resistance contact model is therefore similar to the one described by Wensrich and Katterfeld (2012), except that it is based on a linear model instead of a Hertz model. Note that this model only resists relative bending at the contact point. More complex models that include resistance to bending and twisting have been proposed (see for instance Jiang et al., 2015).
The following plots show the finals state for µ = 0.6 and µr = 0.8 (top and bottom left), and µ = 0.2 and µr = 0.1 (top and bottom right). The balls identified on the free surface are colored green and were found from a fitted cone surface (shown in the bottom plots) function using algorithms available in the SciPy Python module.

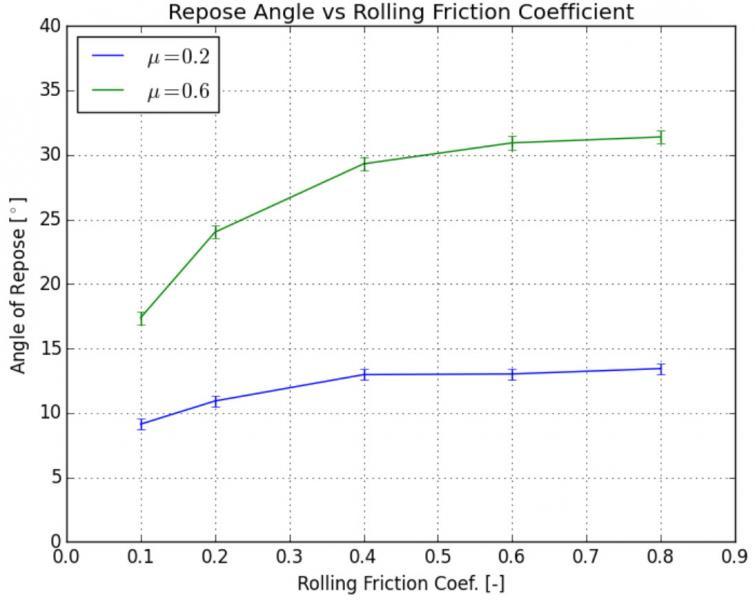
The following figure shows the evolution of the estimated repose angle with increasing rolling friction coefficient, for µ = 0.2 and µ = 0.6. The error bars indicate, for each estimation, the 95% student-t based confidence interval of the estimated value. The results confirm and quantify the trends observed in the 2D model: the repose angle increases with increasing friction and rolling friction coefficients, and for a constant friction coefficient, reaches a plateau when the rolling friction coefficient becomes larger than the friction coefficient. The test should be repeated with different sets of parameters and with different initial geometries of the packing (i.e., different random seed numbers) to obtain better statistics, and an iso-value map of the estimated repose angle could be produced, as done by Wensrich and Katterfeld (2012) for a model similar to the one presented here. Also, other parameters, such as the size of the system, the particle size-distribution, or the properties of the contacts with the base plane will affect the results and this example could easily be augmented to assess their influence.
References
Ai J., J-F Chen, J. M. Rotter, and J. Y. Ooi. (2011) "Assessment of Rolling Resistance Models in Discrete Element Simulations," Powder Technology, 206, 269-282.
Wensrich, C. M., and A. Katterfeld (2012) "Rolling Friction as a Technique for Modelling Particle Shape in DEM," Powder Technology, 217, 409-417.
Iwashita, K., and M. Oda. (1998) "Rolling resistance at contacts in simulation of shear band development by DEM," Journal of Engineering Mechanics ASCE, 124, 285-292.
Jiang, M., J. Wang, and Z. Shen. (2015) "A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances," Computers and Geotechnics, 65, 147-163.
