Dynamic analysis in UDEC permits two-dimensional, plane-strain or plane-stress, fully dynamic analysis. The calculation is based on the explicit finite-difference scheme to solve the full equations of motion using real rigid-block masses, or lumped gridpoint masses derived from the real density of surrounding zones (rather than scaled masses used for static solution).
The dynamic formulation can be coupled to the structural element model, thus permitting analysis of rock-structure interaction brought about by ground shaking. The dynamic feature can also be coupled to the model for fluid flow in joints. This permits, for example, analyzes of the effect of dynamic loading of saturated joints. The dynamic model likewise can be coupled to the optional thermal model in order to calculate the combined effect of thermal and dynamic loading. The dynamic facility expands UDEC’s analytic capability to a wide range of dynamic problems in disciplines such as earthquake engineering, seismology and mine rock bursts.
Dynamic Loading and Boundary Conditions
UDEC models a region of jointed material subjected to external and/or internal dynamic loading by applying a dynamic input boundary condition either at the model boundary or to internal blocks. Wave reflections at model boundaries are minimized by specifying either quiet (viscous) or free-field boundary conditions.
In UDEC, the dynamic input can be applied (using a harmonic function, a table, a history or a UDEC function) in one of four ways:
- A velocity;
- A stress (or pressure);
- A force; or
- A fluid pressure within joints.
Wave Transmission through the Model
Numerical distortion of the propagating wave can occur in a dynamic analysis, whether it is based on a continuum or discontinuum program, as a function of the modeling conditions. Both the frequency content of the input wave and the wave-speed characteristics of the system will affect the numerical accuracy of wave transmission.
The physical stiffness of in-situ joints can have a substantial influence on seismic wave propagation. Pyrak-Nolte et al. (1990) present field and laboratory test results that demonstrate the effect of the stiffness of dry natural fractures in rock on high frequency attenuation and changes in travel time of the seismic wave. It can be important to represent this effect in the discontinuum model if the wave transmission is be to modeled accurately, particularly when the joint spacing is variable.
It is possible to account for this in UDEC by making the blocks deformable (i.e., meshed) with zone sizes accommodating the element size restriction imposed by frequency and wavelength. Kuhlemeyer and Lysmer (1973) show that for accurate representation of wave transmission through a model, the spatial element size must be smaller than approximately one-tenth to one-eighth of the wavelength associated with the highest frequency component of the input wave.
Mechanical Damping
Natural dynamic systems contain some degree of damping of the vibration energy within the system; otherwise, the system would oscillate indefinitely when subjected to driving forces. Damping is due, in part, to energy loss as a result of internal friction in the intact material and slippage along interfaces within the system.
For a dynamic analysis, the damping in the numerical simulation should attempt to reproduce the energy losses in the natural system when subjected to dynamic loading. UDEC uses a dynamic algorithm for solution of two general classes of mechanical problems: quasi-static and dynamic. Damping is used in the solution of both classes of problems, but quasi-static problems require additional damping. Two types of dynamic damping are available in UDEC.
RAYLEIGH DAMPING — In time domain programs, Rayleigh damping is commonly used to provide damping that is approximately frequency-independent over a restricted range of frequencies. Although Rayleigh damping embodies two viscous elements (in which the absorbed energy is dependent on frequency), the frequency-dependent effects are arranged to cancel out at the frequencies of interest.
LOCAL DAMPING — The local damping embodied in UDEC’s static solution scheme may be used dynamically, but with a damping coefficient appropriate to wave propagation. Local damping in dynamic problems is useful as an approximate way to include hysteretic damping for waveforms that are not complex ((i.e., many number of frequency components).
Example
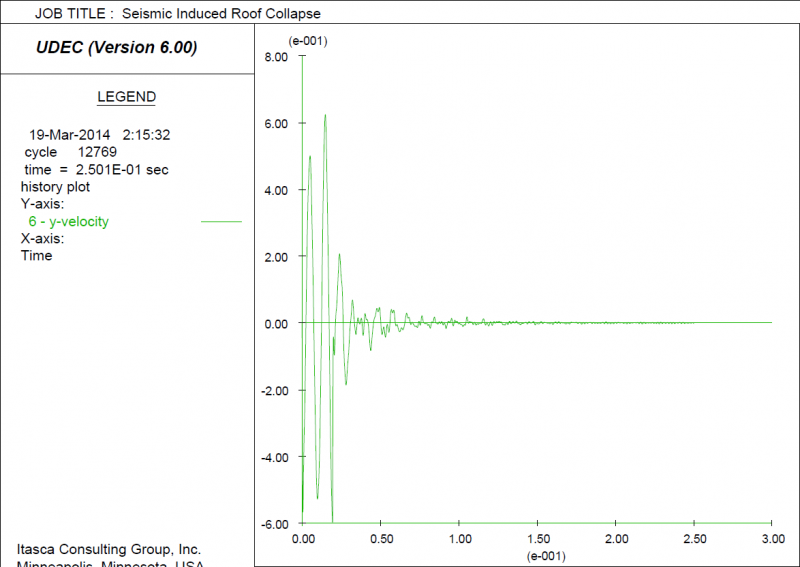
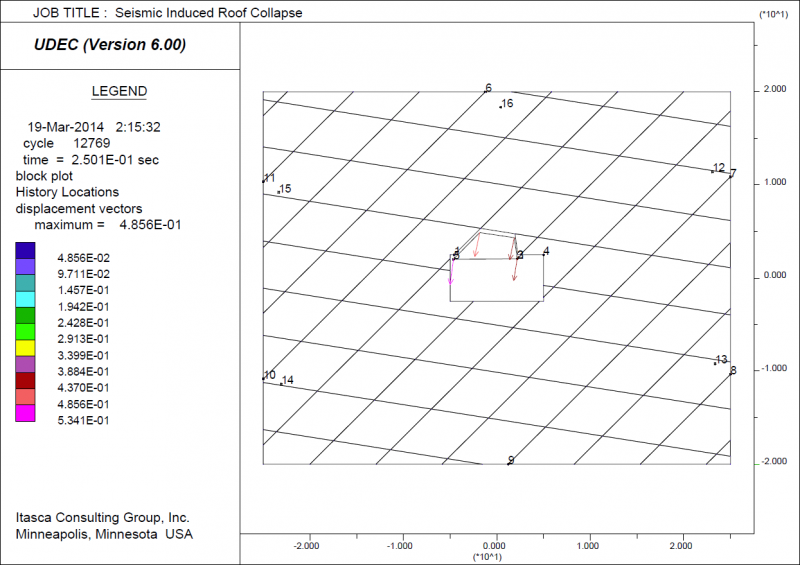
At 800 m underground, a 5-m high and 10-m wide mining over-cut is driven through a rock mass with two continuous joint sets with 5 m-wide spacing. An additional vertical crack has been added to represent some blast damage to the back. Although there is some block movement after mining, the excavation stabilizes. The UDEC model below shows the effect of a seismic event occurring above the over-cut drive, which is represented as an applied stress wave with a peak stress of 12.5 MPa. The y-velocity recorded over the model run at History #6 at the top of the model is shown on the left-hand-side, while the previously stable block from the back can be seen to start falling in the right-hand-side plot.